Глава 6

Всеобщность

Повторение этих линий несет золото;

Построение этого круга на земле

Несет ураганы, бури, громы и молнии.

(К. Марло.) (Трагическая история доктора Фауста)

В нескольких десятках метров от вершины водопада кажется, будто плавно текущий поток предугадывает падение с огромной высоты: вода, содрогаясь, ускоряет свой бег, и, словно крупные пульсирующие вены, в потоке проступают отдельные струи. Неподалеку от потока стоит Митчелл Файгенбаум. Слегка вспотевший в своем пиджаке спортивного покроя и вельветовых брюках, он попыхивает сигарой. Ученый вышел прогуляться с друзьями, но они поторопились уйти вперед, к тихим заводям вверх по течению. Вдруг Файгенбаум начинает быстро вертеть головой, будто болельщик на турнире по пинг-понгу. «Можно сосредоточиться на чем угодно, на островке водяной пены, на любом объекте. Если быстро поворачивать голову, можно разглядеть всю внезапно ставшую различимой структуру поверхности и как бы почувствовать ее внутри себя… — Он делает очередную затяжку. — Впрочем, любой, кто хоть немного понимает в математике, при взгляде на бурную воду, или на облака, клубящиеся одно над другим, или на море во время шторма чувствует, что на самом деле не знает ровным счетом ничего».

Порядок среди хаоса… Так звучит старейший речевой штамп из языка науки. Идея скрытого единства и общей скрытой формы в природе занимала многих и роковым образом вселяла напрасные надежды в чудаков и псевдоученых. Когда Файгенбаум в 1974 г. впервые появился в Национальной лаборатории Лос-Аламоса, через год после того как ему исполнилось тридцать, он знал лишь одно: если физики собираются заняться этим вопросом, им, конечно, понадобится некая практическая основа, способ воплощения идей в вычислениях. Начало этой работы виделось весьма туманно.

Файгенбаума пригласил на работу Питер Каррутерс, спокойный, добродушный с виду ученый-физик, прибывший в 1973 г. из Корнелла, чтобы возглавить теоретический отдел. Первым делом он уволил нескольких сотрудников (Лос-Аламос, в отличие от университетов, не обеспечивает свой персонал должностями на постоянной основе) и заменил их молодыми, подававшими надежды учеными, которых сам же и выбрал. Каррутерс — исследователь, взявший на себя управленческие функции, — был весьма амбициозен, но по собственному опыту знал, что настоящую науку нельзя планировать наперед.

О Файгенбауме его шеф говорил так: «Если бы где-нибудь в верхах, в Вашингтоне, вы заявили: „Турбулентность стоит нам поперек дороги, нам необходимо глубже изучить ее, ибо незнание сводит на нет шансы на прогресс во многих областях“, тогда, конечно, вы набрали бы большую команду и получили финансирование плюс мощный компьютер, способный выполнять объемные программы. И, весьма вероятно, вы ни к чему бы не пришли. И вот вместо всего, о чем я упомянул, у нас есть этот тихий парень. Разумеется, и ему иногда нужны совет и поддержка, но он делает преимущественно все сам». Каррутерс и Файгенбаум не раз обсуждали феномен турбулентности, но с течением времени шеф потерял былую уверенность. Он не совсем понимал, куда клонятся исследования его подчиненного. «Мне казалось, что он решил свернуть дело и обратиться к другим вопросам, но он занимался все той же проблематикой. Ею интересовались во многих научных дисциплинах — именно данным аспектом нелинейных систем. Сейчас уже никто не стал бы утверждать, что верной предпосылкой для их изучения является подготовка в области физики элементарных частиц, теории квантового поля и „групп перенормировки“. Никто даже не подозревал, что необходимо владеть общей теорией стохастических процессов и фрактальными структурами. Митчелл шел по правильному пути. Он предпринял верные действия в нужное время, более того — сделал свою работу первоклассно. Никаких частностей. Было найдено решение для всей проблемы».

Файгенбаум, приехав в Лос-Аламос, был глубоко убежден, что науке, в которой он работал, не удалось проникнуть в сложнейшую область нелинейных проблем. И несмотря на то что он еще ничего не открыл, его интеллект казался многим поразительным. Файгенбаум знал и часто со свойственным ему искусством применял наиболее спорные методы математического анализа, новую технологию вычислений на компьютере, ставившую в тупик большинство его коллег. Ему удалось сохранить веру в некоторые романтические идеи XVIII в., казавшиеся далекими от науки. Он надеялся создать дисциплину, которая стала бы новой, и начал с того, что, отбросив в сторону мысли о сложности реального мира, обратился к самым простым нелинейным уравнениям, какие только мог найти.

Тайны Вселенной впервые заявили о себе четырехлетнему Митчеллу Файгенбауму после войны, через посредство радиоприемника в гостиной его родителей в Бруклине. Его ошеломляла одна мысль о том, что музыка звучит без всяких видимых причин. Это было совсем не то что граммофон. Уж в граммофонах-то Митчелл разбирался! Бабушка разрешала ему запускать проигрыватель на все семьдесят восемь оборотов.

Отец Митчелла, химик по образованию, работал в управлении Нью-Йоркского порта, затем перешел в компанию «Клэрол». Мать преподавала в городской муниципальной школе. Митчелл сначала решил выучиться на инженера-электрика — в Бруклине они зарабатывали неплохо. Затем понял, что предмет его интереса — радио — относится скорее к области физики. Файгенбаум принадлежал к тому поколению физиков, которое выросло во внешних районах Нью-Йорка и достигло больших высот, пройдя через известные муниципальные средние школы (в данном случае школу Самуэла Дж. Тилдена), а затем через Городской колледж.

Получить в Бруклине по-настоящему хорошее образование мог только человек, способный искусно лавировать между миром интеллекта и обыденностью. Мальчик рос невероятно общительным, поэтому, как ему казалось, в детстве его почти не обижали. Однако, осознав, что может и хочет учиться, он стал все больше и больше отдаляться от друзей. Обычные разговоры его уже не интересовали. Правда, был такой момент (случилось это во время последнего года обучения в колледже), когда юноша спохватился: молодость проходит. Митчелл сделал попытку восстановить контакт с окружающими. Он тихо сидел в кафетерии, прислушиваясь к болтовне студентов, и постепенно заново постиг почти всю науку общения с людьми.

Он закончил колледж в 1964 г. и продолжил образование в Массачусетском технологическом институте, где в 1970 г. получил докторскую степень, защитив диссертацию по физике элементарных частиц. Затем прошли четыре бесплодных года в Корнелльском университете и в Политехническом институте Виргинии. Бесплодными они были в смысле публикации работ на общепринятые темы, что представляло немалую важность для молодого университетского ученого: от постдокторантов ожидали в основном написания статей. Время от времени руководитель интересовался у Файгенбаума, как продвигаются дела с той или иной проблемой, и слышал в ответ: «А, это! Мне все понятно».

Каррутерс — ученый, способный на многое, — гордился своим умением отыскивать таланты. Он искал даже не интеллект, а какое-то творческое начало, подобное секрету некой потаенной железы, и всегда вспоминал случай с Кеннетом Вильсоном, еще одним застенчивым физиком из Корнелла, который, как всем казалось, не открыл абсолютно ничего. Между тем каждый, кому удавалось разговорить тихоню, убеждался, что Вильсон видит физику насквозь. Когда встал неизбежный вопрос о заключении бессрочного контракта с Кеном Вильсоном, тех, кто поставил на его скрытый интеллектуальный потенциал, оказалось большинство. Контракт заключили — и последовал взрыв: не две, не три, а целый поток работ буквально хлынул из-под пера Вильсона. Среди них оказалась и та, что принесла ему в 1982 г. Нобелевскую премию.

Вклад Вильсона в физику, наряду с работами двух других исследователей, Лео Каданоффа и Майкла Фишера, явился важнейшей предпосылкой теории хаоса. Каждый из троих, работая самостоятельно, по-своему представлял происходящее при фазовых переходах. Они изучали поведение вещества вблизи точки, где оно переходит из одного состояния в другое: из жидкого в газообразное, из немагнитного в магнитное. Фазовые переходы — своеобразные границы, разделяющие две области существования материи, — в математическом плане характеризуются как в высшей степени нелинейные феномены. Ровное и предсказуемое поведение вещества в одной из фаз обычно мало что дает для понимания переходов в целом. Горшок с водой в печи нагревается вполне стабильно до тех пор, пока не дойдет до точки кипения. Потом изменение температуры замедляется, и на уровне молекулярного взаимодействия жидкости и газа происходит нечто весьма загадочное.

Когда Каданофф занимался этим вопросом в 60-х годах, фазовые переходы ставили ученых в тупик. Представьте себе процесс намагничивания металлического бруска: по мере того как брусок переходит в магнитное состояние, он должен как бы определиться со своей ориентацией, которую выбирает произвольным образом. Этот выбор должна повторить каждая крошечная частица металла. Но как?

В процессе выбора атомы металла должны обмениваться друг с другом определенной информацией. С точки зрения Каданоффа, указанное сообщение наиболее наглядно может быть описано на языке масштабов. В сущности, он предположил, что металл разделен на небольшие ячейки, каждая из которых сообщается со своими ближайшими соседками, причем подобное сообщение можно описать так же, как и взаимодействие любого атома с близлежащими. Отсюда вытекает необходимость масштаба. Наиболее удобно рассматривать металл как фракталоподобную модель, состоящую из ячеек различных размеров.

Теперь для полного воцарения идеи масштабирования требовались математический аппарат и детальное исследование реальных систем. Каданофф чувствовал, что взялся за нелегкое дело, но зато открыл мир изумительной красоты, рожденной универсальностью неписаных природных законов. Универсальность была налицо. Ведь такие, казалось бы, не связанные друг с другом феномены, как кипение жидкостей и намагничивание металлов, подчинялись одним и тем же правилам.

Кеннет Вильсон проделал немалую работу, связавшую все экспериментальные факты воедино в рамках теории «групп перенормировки». Он обеспечил физиков эффективным методом реальных вычислений характеристик реальных систем. Метод перенормировки, появившийся в физике в 40-х годах как раздел квантовой теории, сделал возможным расчеты взаимодействия электронов и протонов. Главной трудностью таких вычислений (как, впрочем, и тех, которые занимали Каданоффа и Вильсона) являлась бесконечность некоторых величин. Борьба с ней была занятием суетным и малоприятным, и Ричард Фейнман, Джулиан Швингер, Фримен Дайсон и другие физики ввели понятие о перенормировке, чтобы освободиться от бесконечностей.

Лишь намного позже, в 60-х годах, Вильсон докопался до причин успеха идеи перенормировки. Как и Каданофф, он размышлял над принципами масштабирования. Определенные характеристики (такие, например, как масса частицы) всегда считались постоянными, как и масса любого предмета, встречающегося нам в повседневной жизни. Принцип масштабирования быстро распространился благодаря тому, что трактовал величины вроде массы отнюдь не как постоянные. Масса и подобные ей характеристики в процессе перенормировки варьируются как в сторону уменьшения, так и в сторону увеличения в зависимости от масштаба, в котором их рассматривают. Эта идея, казавшаяся полной нелепостью, была точным аналогом рассуждений Мандельбро о геометрических формах и береговой линии Великобритании (о том, что их длину невозможно измерить вне зависимости от масштаба). Здесь присутствовала определенная доля относительности. Местоположение наблюдателя — близко ли он, далеко ли, на берегу моря или на космическом спутнике — влияло на результат. Мандельбро также заметил, что наблюдаемые при переходе от одного масштаба к другому перемены подчиняются определенным закономерностям, далеким от произвольности. Изменчивость общепринятых измерений массы или длины говорила о том, что фиксированной остается некая величина иного типа. В случае с фракталами такой величиной было фрактальное измерение — инвариант, который можно рассчитать и использовать в качестве инструмента для дальнейших вычислений. Допущение, что масса может варьироваться в зависимости от масштаба, означало, что математики могут различить феномен подобия невзирая на масштаб явления.

Таким образом, когда возникает необходимость в трудоемких вычислениях, группы перенормировки Вильсона предлагают иной маршрут следования в дебрях сложных проблем. До этого единственным способом изучения в высшей степени нелинейных процессов являлась так называемая теория пертурбаций. Теория эта предполагает, что нелинейная проблема близка к определенной линейной задаче, которая может быть решена, и отстоит от нее лишь на расстояние небольшого «возмущения». Разрешив линейную задачу, мы должны прибегнуть к сложному набору операций с так называемыми диаграммами Фейнмана. Чем точнее нам нужно решить нелинейную задачу, тем больше таких громоздких диаграмм необходимо построить. Если повезет, расчеты приведут нас к решению, но удача — увы! — имеет привычку ускользать всякий раз, когда вопрос особенно интересен. Файгенбаум, как и любой молодой ученый, занимавшийся в 60-х годах физикой частиц, долгими часами строил вышеупомянутые диаграммы. В конечном счете он бросил это занятие, убедившись, что теория пертурбаций скучна, однобока и мало что объясняет. Зато он проникся симпатией к группам перенормировки Вильсона. Они, допуская внутреннее подобие, позволяли устранить некоторые сложности.

На практике же данная теория была не слишком доступной: чтобы выбрать верный способ вычислений и уловить внутреннее подобие, требовалось немало изобретательности. Впрочем, она исправно работала и, как заключил Файгенбаум, даже подвигала физиков на ее применение к проблеме турбулентности. В конце концов внутреннее подобие стало ключом к турбулентности с ее многочисленными колебаниями и завитками. Но о пороге турбулентности, о таинственном моменте, когда упорядоченная система превращается в хаотичную, теория Вильсона как будто ничего не говорила. В частности, не находилось доказательств тому, что данный переход подчиняется закономерностям масштабирования.

Еще в аспирантуре Массачусетского технологического института Файгенбаум приобрел полезный навык, к которому прибегал затем на протяжении многих лет. Однажды он прогуливался с друзьями близ водохранилища Линкольна, что в Бостоне. Привычка гулять по четыре-пять часов выработалась у него давно; она позволяла настраивать мозг на разнообразные впечатления и мысли, приходившие в голову. В тот раз он покинул приятелей и шел один. Миновав группу людей, устроивших в парке пикник, и отдаляясь от них, Митчелл часто оглядывался — прислушивался к звукам голосов, наблюдал жестикуляцию при разговорах, движения рук во время еды. Внезапно он ощутил, что переступает некую границу: фигуры стали слишком крошечными, их действия и движения — бессмысленными, случайными. До него доносились слабые, потерявшие всякий смысл звуки.

Непрестанное движение и непонятная суета жизни… Файгенбаум вспомнил слова Густава Малера. Они выражали те чувства, которые композитор попытался воплотить в третьей части своей Второй симфонии. Словно движения танцующих пар в залитом светом зале, в который вглядываешься из ночной темноты, стоя на расстоянии, откуда музыки уже не слышно… Кажется, что жизнь совсем не имеет смысла. Файгенбаум слушал Малера и вчитывался в Гёте, обуреваемый высокими романтическими порывами. Именно «Фаустом» Гёте он наслаждался больше всего, впитывая мир великого поэта, который сочетал страстность с блестящим умом. Не будь он столь романтически настроен, пожалуй, оставил бы без внимания испытанное им на прогулке смятение. В конце концов, почему бы объектам, рассматриваемым с больших расстояний, не казаться малыми, утратившими свое значение? Физические законы предлагали весьма тривиальное объяснение их сжатия. Однако при более глубоких раздумьях связь между сокращением размеров и потерей объектом своего значения казалась уже не столь очевидной. Почему вещи, уменьшаясь, становятся непостижимыми?

Файгенбаум вполне серьезно попытался осмыслить этот факт с позиций теоретической физики, используя предлагаемый ею научный аппарат. Он задался вопросом, что можно сказать о механизме восприятия человеческого мозга. Предположим, наблюдая за поведением людей, мы делаем о нем определенные выводы. Как человеческий мозг рассортирует огромное количество информации, доступное органам чувств? Ясно — или почти ясно, — что в мозгу не содержится прямых копий окружающего мира. Там не существует «собрания» форм и идей, с которыми можно сравнить воспринимаемые образы. Информация, которая хранится внутри нас, весьма пластична, что делает возможными совершенно фантастические сопоставления и скачки воображения. В ней присутствует доля хаоса. Мозг, кажется, более гибок, чем наводящая в нем порядок классическая физика.

В то же время Файгенбаум размышлял и о феномене цвета. Некоторые дебаты по этому поводу в начале XIX века были вызваны разногласиями последователей Ньютона в Англии и Гёте в Германии. Сторонникам Ньютоновой физики идеи Гёте представлялись околонаучным бредом. Великий немец отказался от рассмотрения цветности как постоянной характеристики, измеряемой с помощью спектрометра и фиксируемой, словно пришпиленная к картону бабочка; по утверждению Гёте, цвет зависит, скорее всего, от восприятия. «Слегка склоняясь то в одну, то в другую сторону, природа колеблется в предписанных ей пределах, — отмечал он, — и таким образом появляются все многообразные состояния явлений, которые представлены нам во времени и пространстве».

Пробным камнем теории Ньютона явился его эксперимент с призмой, которая расщепляет пучок белого света на радугу цветов, распределенных по всему видимому спектру; Ньютон понял, что именно эти чистые цвета должны являться простейшими компонентами, при смешивании которых получается белый цвет. Далее с присущей ему проницательностью он предположил, что цвета соответствуют определенным частотам. По его представлениям, их порождали некие колеблющиеся частицы-корпускулы, воспроизводящие цвета пропорционально скорости колебаний. В эпоху Ньютона подобную идею подтверждало настолько мало доказательств, что она казалась одновременно и неоправданной, и блестящей. Что есть красное? Для физика наших дней это электромагнитное излучение с определенной длиной волны. Он не сомневается, что к настоящему времени верность соображений Ньютона была доказана тысячи раз, тогда как трактат Гёте о феномене цвета благополучно почил в бозе. Когда Файгенбаум занялся поисками, то обнаружил, что одна-единственная копия из библиотеки Гарварда пропала.

Все же отыскав работу, Митчелл выяснил, что Гёте, изучая цвет, провел ряд необычных экспериментов. Начал он, как и Ньютон, с обыкновенной призмы. Ньютон держал призму перед источником света, проецируя расщепляющийся пучок на белую поверхность, Гёте же, приложив призму к глазу, посмотрел сквозь нее и не увидел никакого цвета. Ни радуги, ни отдельных оттенков. Разглядывание сквозь призму белоснежной поверхности или ясного голубого неба давало тот же результат — полное единообразие.

Но если на белой поверхности появлялось едва заметное пятнышко или небо застилали облака, Гёте видел цветовую вспышку. Это дало ему повод заключить, что источником цвета является «чередование света и тени». Он начал исследовать, как люди воспринимают тени, отбрасываемые предметами, которые окрашены в разные цвета. В серии тщательно поставленных опытов использовались свечи и карандаши, зеркала и цветное стекло, свет Луны и Солнца, кристаллы, жидкости и цветные диски. Например, зажигая свечу перед листом белой бумаги в сумерках, экспериментатор держал в руках карандаш. Тень, отбрасываемая карандашом, имела чистый голубой цвет. Почему? Бумага белого цвета воспринимается как белая и в угасающем дневном свете, и в теплом мерцании свечи. Каким образом тень разделяет белое на зоны голубого и красновато-желтого цветов? Цвет, доказывал Гёте, представляет собой «степень темноты, близкую к тени». Переведя это на современный язык, можно сказать, что источник цвета есть состояние границы света и тени и ее особенности.

Так, где Ньютон был редукционистом, Гёте придерживался холизма. Ньютон разбил цвет на составляющие и нашел самое основное физическое объяснение этому феномену. Гёте же, наслаждаясь видами цветущих садов и изучая живописные полотна, искал всеобъемлющее, окончательное толкование интересующего его явления. Ньютон подогнал свою теорию цвета под математическую схему, характерную для всей физики, а Гёте, к счастью или к несчастью, ненавидел математику.

Файгенбаум убедился в том, что идеи Гёте о явлении цвета верны. Эти идеи напомнили ему популярную среди некоторых психологов точку зрения, которая различает суровую реальность и субъективно-изменчивое ее восприятие. Цвета, воспринимаемые человеком, изменяются от случая к случаю, от человека к человеку, в чем несложно убедиться. В понимании Файгенбаума, в идеях Гёте, эмпирических и весьма определенных, таилось гораздо больше истинной научности. Вновь и вновь экспериментатор подчеркивал повторяемость своих опытов, ибо для него именно восприятие цвета являлось всеобщим и объективным. Какие научные доказательства, не зависящие от нашего восприятия, существуют для определимого и реального красного?

Файгенбаум задался вопросом, какого рода математический формализм должен соответствовать человеческому восприятию, особенно тем его видам, которые отсеивают суетное многообразие полученного опыта, обнаруживая всеобщие свойства. Красное не обязательно является светом определенной частоты, как представлялось последователям Ньютона; это территория хаотичного мира, границы которого не так-то просто описать. И все же наш ум находит красное с устойчивым и проверенным постоянством. Таковы были мысли молодого ученого-физика, далекие, казалось бы, от проблем турбулентности в жидкостях. Но все же для постижения механизма отбора человеческим мозгом необходимого в хаосе восприятия первостепенным является понимание того, как беспорядок может породить всеобщность.

Файгенбаум, начав в Лос-Аламосе размышлять над феноменом нелинейности, понял, что из долгих лет своего обучения он, в сущности, не почерпнул ничего полезного. Решить систему нелинейных дифференциальных уравнений, не придерживаясь примеров из учебника, казалось невозможным. Способ пертурбаций с его последовательными корректировками идеализированной задачи, которая, как предполагалось, находится близко к реальной проблеме, выглядел довольно глупым. Ознакомившись с рядом руководств по нелинейным потокам и колебаниям, ученый сделал вывод, что сколько-нибудь разумному физику они мало чем помогут. Имея в своем распоряжении лишь карандаш и бумагу для вычислений, Файгенбаум решил начать с аналога простого уравнения, рассмотренного в свое время Робертом Мэем применительно к биологии популяций.

С таким уравнением — его можно записать как y = r (x — x?) — ученики средней школы знакомятся в курсе алгебры при построения параболы. Каждое значение x дает новое значение y, а полученная в результате кривая выражает связь между x и y в определенном диапазоне значений, при x, меняющемся от нуля до r. Если x (численность популяции в текущем году) мала, то y (численность популяции в следующем году) также будет невелика, но больше, чем x. Кривая резко поднимается вверх. Если значение x находится в середине диапазона, то в этом случае значение y велико. Но парабола выравнивается близ своей вершины и начинает снижаться так, что если значение x велико, значение y вновь мало. Именно это и является эквивалентом скачков численности популяции в экологическом моделировании, предотвращая ничем не ограниченный рост.

Для Мэя, а затем и для Файгенбаума главное заключалось в том, чтобы произвести это простое вычисление не один раз, а повторять его бесконечно, как в «петле обратной связи». Итоги одного подсчета служили исходными данными для следующего. Для графического представления результатов парабола оказывалась незаменимой. Надо было выбрать начальную точку на оси x, провести перпендикуляр вверх до пересечения с параболой, найти соответствующее значение на оси y и принять его за новое значение x. И так далее и тому подобное… Результат сначала будет «скакать» от одной точки к другой, а потом, вероятно, установится на уровне устойчивого равновесия, где значения x и y равны, т. е. численность популяции останется неизменной.

Казалось, нельзя было найти ничего более далекого от сложных расчетов теоретической физики. Вместо единовременного решения запутанной системы одна и та же простая операция повторялась вновь и вновь. Ставящий подобные опыты с числами скорее наблюдатель, словно химик, который следит за ходом реакции, бурлением внутри мензурки. Результат являл собой ряд чисел, не всегда достигавший в итоге стабильного значения: он мог завершиться и скачками значения в некотором интервале, или, как разъяснял Мэй своим коллегам, ряд мог продолжать изменяться совершенно хаотичным образом и настолько долго, насколько хватит терпения за ним наблюдать. Поведение числового ряда зависело от выбранного значения параметра.

Выполняя расчетную часть своих исследований, которую едва ли можно было назвать экспериментом, Файгенбаум одновременно пытался анализировать нелинейные функции с более традиционных, теоретических позиций. Даже тогда он не смог увидеть всю полноту возможностей, которые открывали уравнения. Тем не менее ученый понял, что возможности эти весьма сложны и анализ их окажется довольно трудоемким. Три математика из Лос-Аламоса — Николас Метрополис, Пол Стейн и Майрон Стейн — изучали в 1971 г. похожие алгоритмы, и теперь Пол Стейн предупредил Файгенбаума, что они заставляют поломать голову. Если анализ результатов решения простейшего уравнения оказался столь трудным, чего же было ожидать от гораздо более запутанных формул, которыми описываются реальные системы? И Файгенбаум отложил проблему в долгий ящик.

Этот эпизод из краткой летописи хаоса, история, заварившаяся вокруг одного-единственного, безобидного, на первый взгляд, уравнения, показывает, какими разными глазами ученые смотрят на одну и ту же проблему. Для биологов уравнение было знаком того, что простые системы способны на сложное поведение. Для математиков вопрос заключался в создании совокупности топологических моделей вне всякой связи с численными результатами. Они начинали процедуру «обратной связи» в определенной точке и наблюдали, как следующие одно за другим значения «прыгают» на параболе от ветви к ветви. По мере их движения справа налево ученые фиксировали наблюдаемую последовательность правостороннего (П) и левостороннего (Л) движений: итерация № 1 — П; итерация № 2 — ПЛП; итерация № 193 — ПЛЛЛЛЛППЛЛ… Математику подобные опыты могли поведать много интересного, но физику они казались утомительными и довольно туманными.

В то время никто не догадывался, что Лоренц еще в 1964 г. рассматривал то же уравнение, пытаясь разрешить один вопрос, касавшийся климата. Вопрос этот был столь глубок, что почти никому не приходил в голову. Никто не задумывался, а существует ли климат, можно ли вывести долгосрочные средние значения погодных характеристик для определенных зон земного шара? Тогда, как и сейчас, большинство метеорологов считали, что ответ очевиден: конечно, любая поддающаяся измерению величина — неважно, какие она демонстрирует колебания, — должна иметь некое среднее. Если же вдуматься, все далеко не так ясно. Лоренц указывал, что средняя погода на Земле в течение последних 12 тысяч лет заметно отличалась от средних климатических условий предыдущих 12 тысяч лет, когда почти вся Северная Америка лежала под ледяным покровом. Значило ли это, что переход от одного климата к другому произошел в силу физических причин? Или упомянутые временные отрезки были периодами отклонений от стабильных долгосрочных погодных условий? А может, система, подобная погоде, никогда не усредняется?

Лоренцу не давал покоя еще один вопрос. Допустим, мы можем записать полный набор уравнений, управляющих погодой на земном шаре. Допустим, нам ведомы законы самого Господа Бога. Можем ли мы использовать эти уравнения для расчета среднестатистического уровня температур или осадков? Если уравнения линейные — конечно да. Но они, увы, нелинейны. И Лоренц был вынужден изучить квадратичное разностное уравнение.

Как и Мэй, Лоренц прежде всего выяснил, что происходит, если задавать разные значения параметра. При низких значениях числовой ряд достигал стабильной фиксированной точки, т. е. модель климата вела себя абсолютно предсказуемо: погода никогда не изменялась. Умеренный рост значения параметра провоцировал колебания между двумя точками, но и в этом случае система также усреднялась. За определенной чертой появлялся хаос. Поскольку Лоренц занимался проблемой климата, его интересовало не только то, приведет ли обратная связь к периодическому поведению, — он хотел знать среднее значение полученного результата. Лоренц выяснил, что среднее тоже подвержено колебаниям. При незначительном варьировании параметра оно могло изменяться довольно существенно. Аналогично и земной климат мог никогда не знать прочного равновесия.

Как математический труд статья Лоренца о климате была неудачной. Автор ничего не доказал в общепринятом смысле слова. Как физическое исследование она также не выдерживала критики, ибо не объясняла, почему такая простая модель позволяет сделать выводы о климате земного шара. Однако Лоренц был уверен в своей правоте. «Автор чувствует, что подобное сходство не простая случайность. Нам известно, что разностное уравнение охватывает многое в математике, если не в физике, описывая переходы от одного режима к другому и фактически весь феномен нестабильности». Даже двадцать лет спустя никто не мог понять, какие интуитивные ощущения подвигли Лоренца на публикацию такого отчаянно смелого утверждения в шведском метеорологическом журнале «Теллус». («„Теллус“! Да его же никто не читает!» — с горечью восклицали физики.) Лоренц стоял на пороге глубочайшего проникновения в особенности хаотических систем — слишком глубокого, чтобы сущность его можно было передать на языке метеорологии.

Продолжая изучать изменчивые лики динамических систем, Лоренц осознал, что зависимости чуть более сложные, чем квадратичная, способны внезапно обнаруживать иные типы структур. Внутри отдельно взятой системы нередко таилось не одно устойчивое решение. Если система довольно долго демонстрировала лишь один тип поведения, это не означало, что ей в равной мере не присущ совершенно иной тип поведения. Подобные системы именуют непереходными (интранзитивными); они могут находиться или в одном, или в другом состоянии равновесия, но никак не в обоих сразу, и лишь толчок извне способен заставить систему изменить свое состояние. Если искать примеры в обыденной реальности, часы с маятником являются как раз интранзитивной системой. Энергия поступает в нее постоянно от подвеса или от батареи через механизм регулятора хода, и с тем же постоянством энергия уходит из системы из-за потерь на трение. Очевидным состоянием равновесия являются устойчивые колебательные движения. Если кто-то, проходя мимо, толкнет часы, скорость колебаний маятника от кратковременного толчка увеличится или уменьшится, но он быстро вернется в состояние равновесия. Наряду с первым часы испытывают и другое равновесное состояние (второе решение для уравнений их движения), когда маятник висит неподвижно. Менее тривиальной интранзитивной системой, которой, возможно, свойственно несколько четко обозначенных и совершенно различных вариантов поведения, является климат.

Ученым, изучающим климат и использующим компьютерные программы для моделирования долгосрочного поведения атмосферы и гидросферы Земли, уже несколько лет назад стало известно, что их модели способны демонстрировать как минимум два состояния равновесия, различающихся коренным образом. Один из этих сценариев, весьма драматический, не был реализован ни в одну из минувших геологических эпох. Как бы то ни было, он остается вторым верным решением системы уравнений, управляющих земной погодой. Некоторые специалисты называют его климатом Белой Земли — планеты, континенты которой погребены под снегами, а океаны скованы льдом. Ледовая корка отражала бы около 70 % солнечных лучей и оставалась бы чрезвычайно холодной. Нижний слой атмосферы — тропосфера — был бы гораздо тоньше. Штормы, проносившиеся над шапками снега и глыбами льда, уступали бы по силе тем бурям, что мы наблюдаем сейчас. В общем, подобный климат гораздо менее располагал бы к появлению и развитию жизни, чем реальный. Компьютерные модели настолько часто приходят к состоянию Белой Земли, что ученые сами удивляются, почему оно никогда не наступало. Вероятно, это лишь дело случая.

Для того чтобы вся Земля оделась во льды, необходим мощный толчок извне. Но Лоренц описал еще один тип поведения, названный им «квазиинтранзитивностью». В течение длительного времени система ведет себя примерно одинаково, флуктуации остаются в определенных границах; затем, без какой бы то ни было причины, система резко меняет свое поведение, все еще колеблясь, но обнаруживая уже другое среднее. Создатели компьютерных моделей прекрасно знают об открытии Лоренца, но стараются любой ценой избежать квазиинтранзитивности, поскольку она слишком непредсказуема. Ученые стремятся строить модели, тяготеющие к тому равновесию, которое мы наблюдаем каждый день в реальной жизни. Значительные перемены в погодных условиях они склонны объяснять внешними причинами, например изменением орбиты обращающейся вокруг Солнца планеты. И все же не нужно много фантазии, чтобы увидеть в квазиинтранзитивности вполне убедительные объяснения того, почему в истории Земли случались ледниковые периоды, наступавшие через случайные интервалы времени. Если это объяснение действительно справедливо, нет нужды доискиваться до физических предпосылок оледенения. Ледниковый период может быть побочным продуктом хаоса.

Как коллекционер огнестрельного оружия в эпоху автоматов и базук с тоской вспоминает «кольт» сорок пятого калибра, так и в глубине души современного ученого таится легкая ностальгия по ручному калькулятору модели НР-65. За несколько лет полного господства этому вычислительному устройству удалось навсегда изменить привычки многих исследователей. Для Файгенбаума же счетная машина перекинула мостик от карандаша и бумаги к компьютеру, не сразу оцененному по достоинству служителями науки.

Он еще ничего не знал о Лоренце, но летом 1975 г. на встрече в Аспене, штат Колорадо, услышал рассуждения Стива Смэйла о некоторых свойствах квадратичных разностных уравнений. Смэйл считал открытием некоторые весьма волнующие вопросы о переходе модели от периодичного к хаотическому состоянию. Он не утратил свое отменное чутье на действительно стоящие проблемы. Файгенбаум решил взглянуть на уравнение еще раз. Вооружившись калькулятором, он применил сочетание аналитической алгебры и численных методов, чтобы обозреть свою модель, и главным образом — пограничную зону между хаосом и стабильностью.

В поисках аналогий Файгенбаум мог обратиться к той таинственной границе, что отделяет плавное течение жидкости от турбулентного. Именно к данному участку Роберт Мэй пытался привлечь внимание биологов, которые не замечали, что популяции животных переживают не одни лишь упорядоченные циклы. На пути к хаосу в указанной зоне возникает целый каскад раздвоения периодов: расщепление двух на четыре, четырех — на восемь и т. д., представляющее собой весьма удивительную картину. Именно в точках бифуркации некоторое увеличение плодовитости особей могло привести к смене четырехгодичного цикла популяции непарного шелкопряда восьмигодичным. Файгенбаум решил начать с подсчета точных значений параметра, порождавших расщепления.

В конце концов к открытию ученого привело, как ни странно, низкое быстродействие калькулятора. Казалось, расчеты точного значения параметра для каждого удвоения периодов растягиваются на века, хотя на самом деле вычисления занимали считанные минуты. Однако чем выше поднимался Файгенбаум по цепочке циклов, тем больше времени требовали операции с числами. Имей ученый мощный компьютер и печатающее устройство, он, пожалуй, не заметил бы никакой закономерности, но ему приходилось записывать результаты вручную и, пока калькулятор работал, размышлять над ними. Чтобы сэкономить время, он просто-напросто пытался угадать, каким будет следующее значение.

И вдруг Файгенбаум увидел, что гадать уже незачем. В системе пряталась неожиданная упорядоченность, числа приближались друг к другу, словно столбы высоковольтной линии, сходящиеся на горизонте в точку, — удвоения периодов не просто ускорялись, а ускорялись с постоянным коэффициентом.

Почему так происходило? Обычно появление геометрической сходимости предполагает, что в определенном месте некий объект повторяет сам себя в различных масштабах. Если внутри изучаемой системы таилась подобная масштабная модель, это было очень любопытно. Никто еще такого не наблюдал. Файгенбаум, рассчитав коэффициент конвергенции с наибольшей точностью, какая могла быть достигнута с имевшимся у него калькулятором (три цифры после запятой), получил следующий результат: 4,669. Имел ли данный коэффициент какой-либо математический смысл? Файгенбаум сделал то, что на его месте сделал бы любой ученый, хоть немного интересующийся числами: он провел остаток дня, пытаясь подогнать получившийся итог под известные постоянные: ?, e и другие, но это ни к чему его не привело.

Удивительно, но позже Роберт Мэй понял, что он тоже наблюдал подобную геометрическую сходимость, однако забыл о ней столь же быстро, сколь мимолетно она промелькнула перед его глазами. С точки зрения эколога, это был не более чем специфический вычислительный эффект. В системах реального мира — популяциях животных и даже в некоторых экономических моделях — любые четкие закономерности неизбежно исчезали в шумах. Та самая неупорядоченность, которая до сих пор служила ученому путеводной нитью, заставила его остановиться на пороге открытия. Никогда бы ему не пришло в голову, что числовые тонкости столь важны.

Но Файгенбаум прекрасно понимал, к чему привели его вычисления, поскольку геометрическая сходимость указывала на присутствие в уравнении чего-то масштабного, а Митчелл в полной мере сознавал существенность масштаба, от которого, по сути, зависела вся теория перенормировки. В явно неуправляемой системе масштабность свидетельствовала о том, что определенное качество сохраняется, в то время как все остальные претерпевают изменения. Итак, где-то в изучаемом уравнения пряталась упорядоченность. Но где именно? Куда идти дальше, сказать было сложно.

Лето быстро сменяется осенью, которая сильно чувствуется в разреженном воздухе Лос-Аламоса. Уже подходил к концу октябрь, когда Файгенбауму пришла в голову странная мысль. Он знал, что Метрополис, Пол Стейн и Майрон Стейн, рассматривая описанное выше уравнение и другие, выяснили, что определенное поведение повторяется при переходе от одного типа функции к другому. Обнаруживались те же сочетания знаков «П» и «Л», причем в том же порядке. Одна из исследованных ранее функций включала синус, из-за чего тщательно разработанный Файгенбаумом подход к изучению параболы оказался неподходящим. Ему пришлось начать заново; вновь используя свой НР-65, он начал рассчитывать удвоения периодов для функции x_t+1 = r sin ?х_t. Расчет тригонометрической функции значительно замедлял вычислительную процедуру, и Файгенбауму пришла мысль использовать сокращенный вариант уравнения. И вновь, задав наибольшую возможную точность, он получил результат с тремя цифрами после запятой: 4,669.

То же число! Невероятно, но данная тригонометрическая функция не просто обнаруживала последовательную геометрическую регулярность. Наблюдаемый эффект оказался численно идентичным упорядоченности гораздо более простой функции! Ни математика, ни физика не объясняли, каким образом два столь различных по форме уравнения приводили к одинаковому результату.

Файгенбаум связался с Полом Стейном, но тот не поверил в подобное совпадение, посчитав доказательства недостаточными, — в конце концов, точность калькулятора оставляла желать лучшего. Несмотря на это Файгенбаум позвонил своим родителям в Нью-Джерси и сообщил, что столкнулся в своих исследованиях с весьма глубоким вопросом. Этот вопрос, объявил он матери, скоро сделает его, Файгенбаума, знаменитым. Затем он приступил к изучению других функций — всех, которые, по его мнению, также проходили через последовательность разветвлений на пути к хаосу. Вычисления давали неизменно тот же итог — 4,669.

Файгенбаум имел дело с цифрами всю свою жизнь. Еще подростком он научился рассчитывать логарифмы и значения синусов, которые все остальные искали в таблицах. Вместе с тем он даже не представлял, как использовать в исследованиях иное счетное устройство, кроме ручного калькулятора. Митчелл относился к тем многочисленным физикам и математикам, которые презирали свойственное компьютеру механистическое мышление. И вот час компьютера пробил! Файгенбаум обратился к коллеге с просьбой научить его программированию на Фортране и уже к вечеру для каждой из множества взятых им функций подсчитал свою постоянную с точностью до пяти цифр после запятой — 4,66920. Проштудировав ночью правила вычислений с двойной точностью, Файгенбаум на следующий день получил значение 4,6692016090. Этого было достаточно, чтобы убедить Стейна, но самого Митчелла все еще одолевали сомнения. Он намеревался искать упорядоченность — квинтэссенцию математики. Однако, приступая к делу, ученый уже знал, что некоторым типам уравнений, как и отдельным физическим системам, присущи особые свойства. Конечно, уравнения были довольно простыми — квадратичные и тригонометрические, функционально разные, но вполне тривиальные с математической точки зрения. И все же содержалось в них нечто такое, что из раза в раз рождало одно-единственное число. Что это, гадал Файгенбаум, игра случая — шутка мироздания или новый закон природы?

Представьте себе такую ситуацию: доисторический мыслитель обнаружил, что некоторые объекты тяжелее всех остальных и обладают неким абстрактным качеством, которое он назвал весом. Конечно же, сию мысль необходимо научно обосновать. Наш экспериментатор на самом деле никогда еще не измерял вес, но вроде бы кое-что ему понятно. Он смотрит на огромных змей и крошечных змеек, на больших медведей и маленьких медвежат и догадывается, что размер животного, должно быть, связан каким-то образом с его весом. Построив весы, он начинает взвешивать змей. К его удивлению, все змеи весят одинаково. С медведями та же история, но что удивительнее всего — косолапые весят столько же, сколько змеи — 4,6692016090! Ясно одно: вес является вовсе не тем, что полагал пытливый ум. Вся идея требует переосмысления.

Струящиеся ручьи, качающиеся маятники, электронные осцилляторы и множество других физических систем испытывают переход на пути к хаосу. Хотя такие переходы весьма сложны для анализа, механизмы функционирования систем довольно хорошо изучены. Физики знают уравнения, которые описывают эти системы, но перебросить мост от уравнений различного вида к глобальному долгосрочному поведению объектов не удается. Открытие Файгенбаума подсказывало, что дело не в уравнениях: с появлением порядка вид уравнения терял свою значимость, и независимо от него результат получался один и тот же. «Традиция физики такова, что мы обособляем и детализируем механизмы явления, а затем исследуем их по отдельности, — пояснял Файгенбаум. — В данном же случае мы знаем верные уравнения, но они нам не помогут. Суммировав все микроскопические фрагменты, мы выясним, что не можем распространить их на длительный период, потому что не они важны в интересующей нас проблеме. И это коренным образом меняет смысл выражения знать что-либо».

И хотя связь между вычислениями и физикой казалась весьма проблематичной, Файгенбаум понял, что должен искать новый способ расчетов сложных нелинейных проблем. До сих пор он занимался перебором различных функций, пытаясь подыскать среди них подходящую для моделирования систем. Открытие некой всеобщности означало, что избранный путь ведет в никуда. Регулярность никоим образом не касалась синусов, не имела ничего общего с параболами или с другими отдельно взятыми функциями. Почему? Это был шок! Природа, на мгновение отдернув занавес, позволила нам украдкой взглянуть на неожиданную упорядоченность. Но что еще пряталось за покровом тайны?

Озарение явилось Файгенбауму в образе двух небольших волнистых форм и еще одной, покрупнее. И ничего больше. Лишь яркое и четкое изображение, словно врезавшееся в сознание. Верхушка айсберга, отголосок мыслительных процессов, происходивших где-то на уровне подсознания; он был связан с масштабированием и указывал верный путь.

Файгенбаум изучал аттракторы. Устойчивое равновесие, о котором говорили его графики, являлось фиксированной точкой, притягивавшей, в свою очередь, другие. Не имело значения, какова начальная «популяция», — она все равно неуклонно приближалась к аттрактору. Затем, с первым раздвоением периодов, аттрактор, подобно делящейся клетке, раздваивался. Первоначально две эти точки находились совсем рядом, но по мере роста значения параметра они отдалялись друг от друга. Затем происходило следующее расщепление периодов, и каждая точка аттрактора вновь начинала делиться. Число — инвариант, полученный Файгенбаумом, — позволило ему предугадывать, когда именно это произойдет. Ученый обнаружил, что может прогнозировать этот эффект для сложнейшего аттрактора — в двух, четырех, восьми точках… Говоря языком экологии, он мог прогнозировать действительную численность, которая достигается в популяциях во время ежегодных колебаний. Кроме того, здесь наблюдалась некая сходимость: все числа также подчинялись закону масштаба.

Файгенбаум занимался изучением давно забытой пограничной области между физикой и математикой. Какой из двух дисциплин принадлежит его работа, определить было нелегко. С одной стороны, его труд не принадлежал математике, ибо ничего не доказывал. Конечно, ученый оперировал числами, но математик относится к ним так же, как банкир к мешкам со звонкой монетой. Номинально эти металлические кругляши — предмет труда финансиста, но они мелковаты, и возни с ними не оберешься. Идеи — вот настоящая валюта математики! Изыскания Файгенбаума относились скорее к области физики, причем, как ни странно, физики экспериментальной.

Не мезоны и кварки, а числа и функции являлись объектом внимания ученого. Они тоже имели траектории и орбиты. Ему приходилось исследовать их поведение. Используя термин, который позже станет ходовым в новой науке, можно сказать, что Файгенбауму требовалось добиться интуитивного прозрения, которое отлилось бы в теорию и методологию. Спектрометр, ускоритель частиц и пузырьковую камеру ему заменил компьютер. Обычно пользователь формулирует задачу, программирует ее, вводит в вычислительную машину и ждет решения — одного для каждой конкретной проблемы. Файгенбаум и те, кто шел по его стопам, нуждались в большем. Требовалось повторить проделанное Лоренцем — создать миниатюрные вселенные и наблюдать за их эволюцией. Затем, меняя то или иное свойство, исследователи могли проследить, как меняются пути развития. В конечном счете они убедились, что крошечные изменения определенных качеств могут повлечь за собой значительные метаморфозы поведения системы в целом.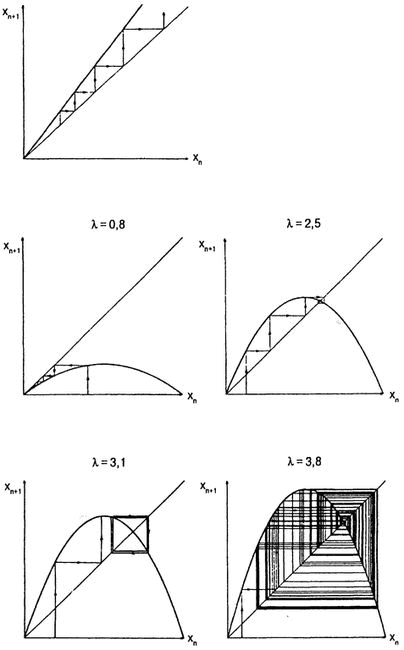

^{Рис. 6.1. Хаос под микроскопом. Простое уравнение, повторяемое много раз. Файгенбаум сосредоточился на линейных функциях, вычисляя значение одной величины в зависимости от значения другой. Для Популяций животного мира функция выражала соотношение между численностью в текущем и следующем году. Одним из способов наглядного представления таких функций является построение графика, где исходные данные отмечаются на горизонтальной оси, а конечные — на вертикальной. Для каждого значения x существует лишь одно значение y, и оба они образуют форму, представленную сплошной линией. Затем, чтобы изобразить долгосрочное поведение системы, Файгенбаум вычертил траекторию, начинавшуюся с произвольно взятого значения x. Поскольку каждое значение у вновь подставлялось в ту же функцию в качестве новой исходной величины, ученый мог применить нечто вроде схематичного сокращения. Траектория скачками отдалялась от прямой, проведенной под углом 45°, где значения x и y равны. Для эколога наиболее очевидным типом функции, отображающей рост популяции, будет линейная — мальтузианская схема устойчивого и ничем не ограниченного увеличения с фиксированным ежегодным приростом (вверху слева). Более «реалистичные» функции представляют собой дугу, демонстрируя популяции. Здесь изображена так называемая логистическая карта для параболы, заданной функцией y = rx (1-x), где параметр r меняется от 0 до 4, определяя крутизну параболы. Но, как выяснил Файгенбаум, вид функции не имел значения. Действительно важным оказалось наличие у нее выпуклости. Поведение существенно зависело и от того, насколько парабола крута — от степени нелинейности, которую Роберт Мэй назвал «взлетами и падениями» (т. е. от способности живущей в естественных условиях популяции к увеличению и снижению числа составляющих ее особей). Слишком низкая парабола означала вымирание: любое начальное значение фактически приводило к нулю. Увеличение степени крутизны порождало устойчивое равновесие — ситуацию, понятную для эколога, который придерживается традиционных взглядов. Точка равновесия, находясь на любой траектории, являлась одномерным аттрактором. После определенной точки начинались разветвления, порождающие колеблющуюся популяцию с двумя периодами. Затем опять происходило удвоение периода, и еще, и еще раз, так что в конце концов траектория «успокаивалась» (внизу справа). Когда Файгенбаум попытался создать новую теорию, подобные изображения послужили ему отправной точкой. Он начал размышлять на языке итераций: функции функций, функции функций от функций и т. д.; схемы с двумя «горбами», потом с четырьмя…}

Файгенбаум быстро выяснил, что компьютеры Лос-Аламоса мало подходят для вычислений, которые он задумал. Несмотря на огромные ресурсы лаборатории, гораздо более обширные, нежели в большинстве университетов, лишь несколько терминалов могли воспроизводить графики и изображения, да и те находились в отделе вооружения. Файгенбаум намеревался наносить определенные числа в виде точек на своеобразную карту и вынужден был прибегнуть к наиболее простому из возможных методов: он использовал длинные рулоны распечаток, где просматривались линии, составленные из чередующихся пробелов, звездочек и знаков сложения. Официальная политика лаборатории заключалась в том, что один большой компьютер лучше нескольких менее мощных. Это было следствие курса «одна проблема — одно решение». Маломощные машины отбивали всякую охоту к исследованиям; к тому же, приобретая компьютер, каждый отдел должен был следовать обязательным указаниям сверху и давать в этом отчет. Лишь гораздо позже, благодаря финансовой помощи теоретического отдела, Файгенбаум получил в личное пользование вычислительную машину стоимостью 20 000 долларов. Теперь он мог видоизменять свои уравнения и мелькавшие на экране картины, перестраивать их, играя на компьютере, словно на музыкальном инструменте. Но это было позже, а пока единственные терминалы, за которыми удавалось всерьез работать с графикой, находились в строго охраняемых зонах, как говорили в лаборатории — за забором. Файгенбауму приходилось использовать терминал, соединенный телефонными кабелями с центральным компьютером. Имея дело с таким устройством, оценить истинную мощность машины на другом конце кабеля весьма сложно, — даже решение простейших задач занимало целые минуты. Чтобы отредактировать лишь одну строчку программы, приходилось, нажав клавишу «Возврат», ждать под непрерывный гул терминала, пока центральный компьютер не обслужит других пользователей.

Вычисляя, Файгенбаум непрерывно размышлял. Какая еще неизвестная математика могла породить наблюдаемые им множественные масштабные модели? Он понял: нечто в этих функциях должно быть повторяющимся, самовоспроизводящимся. Поведением исследуемой системы руководило поведение другой, скрытой внутри нее. Волнистый контур, открывшийся ученому в миг озарения, кое-что прояснял в том, как масштаб одной функции мог быть подогнан в соответствие с другой функцией. Файгенбаум применил теорию групп перенормировки, прибегнув к масштабированию, чтобы избавиться от бесконечности и получить количественные оценки. Весной 1976 г. его жизнь обрела безумный ритм, какого он не знал прежде. Погрузившись в некий транс, Файгенбаум с каким-то неистовством писал программы, что-то черкал карандашом на бумаге и вновь программировал. Он даже не обращался за помощью в компьютерный отдел: это было бы равносильно отказу от собственного компьютера и замене его телефоном, а перестройка метода работы казалась весьма рискованной. Митчелл не прерывался более чем на пять минут, иначе компьютер автоматически отключил бы его линию. Все же временами машина подводила ученого, повергая его в состояние, близкое к шоку. Так, без перерыва, он работал больше двух месяцев. Его рабочий день длился двадцать два часа. Когда он ложился спать, напряжение не покидало его, поднимая ровно через сто двадцать минут и заставляя думать с того же места, где он остановился. Силы его поддерживал лишь кофе. (Даже в лучшие времена Файгенбаум существовал исключительно на полусырых бифштексах, кофе и красном вине. Друзья подшучивали, что он получает витамины из сигарет.)

Конец этому положил врач, прописав ученому успокоительное в скромных дозах и усиленный отдых. Но к тому времени Файгенбаум уже создал универсальную теорию.

Универсальность стирала грань между прекрасным и полезным. Математиков, которые перешли определенную черту, мало волнует пригодность их теорий для вычислений, физики же, миновав некую точку, нуждаются в числах. Всеобщность вселяла надежду на то, что, решив легкую задачу, физики смогут ответить на гораздо более сложные вопросы, поскольку решения будут идентичными. Встроив свое открытие в рамки групп перенормировки, Файгенбаум придал теории такой облик, что физики могли признать ее в качестве почти стандартного инструмента вычислений.

Но то полезное, что присутствовало в новой теории, одновременно делало ее и весьма сомнительной для физиков. Всеобщность означала, что различные системы ведут себя одинаково. Безусловно, Файгенбаум лишь изучал простые функции. Впрочем, он держался того мнения, что его теория отражает естественный закон, который относится ко всем системам, испытывающим переход от упорядоченного состояния к турбулентному. Все знали, что турбулентность представляет собой непрерывный спектр различных частот, но откуда они появлялись, оставалось загадкой. И вдруг удалось увидеть их последовательно появляющимися друг за другом! Физический подтекст заключался в том, что системы реального мира вели себя точно так же и их поведение можно было измерить. Универсальность Файгенбаума являлась не только качественной, но и количественной характеристикой, не только структурной, но и метрической.

Прошли годы, а Файгенбаум все еще хранил в ящике стола письма с вежливыми отказами в публикации статей. Тогда он уже в полной мере достиг славы и признания; работа, написанная в Лос-Аламосе, принесла ему награды и премии, которые, в свою очередь, означали престиж и немалые деньги. Но ученый все еще терзался тем, что редакторы главных научных журналов в течение двух долгих лет отказывают ему в публикации. Трудно поверить, что причиной отказа послужила невероятная оригинальность открытия. Современная наука с ее огромными потоками информации и беспристрастной манерой вдумчивого суждения не допускает предпочтений. И тем не менее… Один из издателей, вернувших Файгенбауму его рукопись, позже признался, что в самом деле отверг работу, ставшую поворотным пунктом в развитии науки. При этом он продолжал настаивать, что статья не очень отвечала профилю издания, каковым являлась прикладная математика. Между тем, несмотря на отсутствие публикаций, открытие Файгенбаума вызвало широкий резонанс в кругах математиков и физиков. Важнейшие пункты его теории стали известны из лекций и препринтов, как это часто и случается в современном научном мире. Файгенбаум рассказывал о своих исследованиях на конференциях, а просьбы предоставить копии статей, приходившие сначала десятками, позже буквально потекли рекой.

Сегодняшняя экономика в значительной степени зависит от эффективности теорий рынка. Предполагается, что знания циркулируют довольно свободно. По общему мнению, принимающие важные решения люди имеют доступ примерно к одной и той же совокупности данных. Бесспорно, не обходится без некоторых пробелов в знаниях или использования неких скрытых сведений. Так или иначе, ученые считают единожды обнародованную информацию известной везде. У историков науки на сей счет есть собственная концепция: каждое новое открытие, каждая новая идея сразу же причисляется к общему достоянию научного мира. Любой прорыв, озарение основаны на прошлом знании. Наука растет, словно дом, кирпичик за кирпичиком. Для целей практики можно считать, что научный прогресс движется поступательно и линейно.

Подобный взгляд на науку верен, когда все ожидают решения четко обозначенной проблемы в совершенно определенной области. В частности, открытие молекулярной структуры ДНК было правильно принято всеми. Но история распространения новых идей далеко не всегда столь безоблачна. Когда в недрах различных дисциплин возникли странные гипотезы о нелинейности, поток мысли уже проложил себе русла, не предусмотренные стандартной логикой историков. История науки о хаосе не только история новых теорий и неожиданных открытий, но и история запоздалого постижения забытых истин. Многие детали головоломки, замеченные еще Пуанкаре, Максвеллом, Эйнштейном, были отброшены и забыты. Новые элементы оказались доступны пониманию немногих. Относящееся к математике восприняли представители этой науки, физики извлекли что-то свое, а новое в метеорологии не заметил вообще никто. Укоренение новых идей в умах протекало так же нелегко, как и появление их на свет.

Каждый ученый — метеор, рожденный особым созвездием своих интеллектуальных предшественников. Каждый странствует в своем мире идей, и эти миры так или иначе ограничены. Знания несовершенны. Ученые подвержены влиянию традиций тех наук, которым они служат, или образования. Научный мир может быть удивительно консервативным. Историю в новое русло направляет отнюдь не собрание ученых мужей, а горсточка индивидов — носителей особого восприятия, особых целей.

Впоследствии оформился общий взгляд на то, чьи новации, чья роль важнее всего. Однако тут не обошлось без ревизионизма. В самый разгар становления новой науки, особенно в конце 70-х годов, вы не сыскали бы двух физиков или двух математиков, одинаково воспринимавших феномен хаоса. Тот, кто привык к классическим системам без трения или диссипации, принимал сторону русских ученых А. Н. Колмогорова и В. И. Арнольда. Специалисты, изучающие классические динамические системы, числили своими соратниками Пуанкаре и Биркхофа, Левинсона и Смэйла. Позже основная масса математиков отдала предпочтение Смэйлу, Гукенхаймеру и Руэллю, а также плеяде исследователей из Лос-Аламоса: Уламу, Метрополису, Стейну. Физик-теоретик выше всего ставил Руэлля, Лоренца, Ресслера и Йорка, биолог — Смэйла, Гукенхаймера, Мэя и Йорка. Число подобных комбинаций бесконечно; например, геолог или сейсмолог признавал прямое влияние идей Мандельбро, а физик-теоретик и имени-то такого, возможно, не слышал.

Роль Файгенбаума стала предметом ожесточенных споров. Много позже, когда слава его уже пошла на убыль, некоторые физики начали цитировать других ученых, работавших над тем же вопросом приблизительно в то же время. Некоторые обвиняли Файгенбаума в том, что он сосредоточился на слишком узком фрагменте широчайшего спектра хаотичного поведения. Как сказал бы физик, «файгенбаумологию» явно переоценили; разумеется, это прекрасная статья, но не настолько поворотная, как, например, работа Йорка. В 1984 г. Файгенбаума пригласили выступить на Нобелевском семинаре в Швеции, где разгорелись жаркие дискуссии. Бенуа Мандельбро, настроенный явно не самым лучшим образом, сделал доклад, о котором позже вспоминали как о «лекции против Файгенбаума». Откопав где-то работу об удвоении периодов, написанную двадцать один год назад финским математиком Мирбергом, он перекрестил последовательности Файгенбаума в «ряды Мирберга».

Как бы то ни было, именно Файгенбаум открыл всеобщность и создал теорию, ставшую точкой опоры для новой дисциплины. Не имея возможности опубликовать столь поразительные и кажущиеся противоречивыми результаты, он включил их в доклад на конференции в Нью-Хэмпшире в августе 1976 г., рассказывал о своей работе на международном заседании математиков в Лос-Аламосе в сентябре, беседовал о ней на встречах в университете Брауна. Как само открытие, так и сопутствующая ему теория вызывали удивление, недоверие, восторг. Чем больше ученые размышляли о явлении нелинейности, тем сильнее ощущали истинную власть универсальности Файгенбаума. Один из них, не мудрствуя лукаво, отметил: «Это открытие стало для нас одновременно и радостным, и шокирующим. В нелинейных системах присутствовали структуры, которые, если рассматривать их правильно, всегда являются одинаковыми». Некоторые физики позаимствовали как саму идею, так и методы Файгенбаума. Используя простейшие счетные машинки, они могли испытать то же изумление и удовлетворение, которое он чувствовал в Лос-Аламосе. Эти специалисты совершенствовали новый метод. Прослушав доклад Файгенбаума в Принстоне, в Институте перспективных исследований, Предраг Свитанович, специалист по физике частиц, помог ему упростить теорию и расширить ее универсальность, но сделал вид, что занимается этим лишь для развлечения, — стеснялся посвятить коллег в эту работу.

Большинство математиков также весьма сдержанно отнеслись к новой теории, главным образом потому, что Файгенбаум пренебрег точными доказательствами. Действительно, их не существовало до 1979 г., когда появилась работа Оскара Е. Ленфорда-третьего. Файгенбаум часто вспоминал о своем выступлении перед именитой аудиторией, собравшейся в сентябре в Лос-Аламосе: не успел он начать, как выдающийся математик Марк Кац, поднявшись, спросил: «Вы намерены предложить нам числа или все же доказательство?» «Больше, чем первое, но меньше, чем второе», — ответил Файгенбаум. «И подобное разумный человек называет доказательством?»

Файгенбаум предложил подождать суждения слушателей. Когда доклад подошел к концу, ученый осведомился о мнении Каца. Тот, сардонически упирая на звук «р», произнес: «Да, пожалуй, это действительно доказательство р-разумного человека, а детали пусть останутся точной математике».

Движение уже началось. Открытие всеобщности лишь подтолкнуло его. Летом 1977 г. двое физиков, Джозеф Форд и Джулио Казати, организовали первую конференцию, посвященную хаосу. Она проходила в Италии, на живописной вилле в маленьком городке Комо, находящемся южнее одноименного озера, удивительного прозрачно-голубого вместилища талых альпийских снегов. Около ста человек приехали туда — преимущественно физики, но попадались и представители других дисциплин.

«Митч, разглядев универсальность, выяснил, как она сводится к определенному масштабу, и расчистил путь к хаосу, привлекающий каждого уже на уровне интуиции, — заметил Форд. — Впервые у нас появилась четкая модель, понять которую сможет каждый. Практически всюду, начиная от астрономии и заканчивая зоологией, ученые занимались подобными исследованиями, направляли свои статьи в узкоспециальные журналы и даже не догадывались, что многие вокруг делают то же самое. Каждый думал, что он одинок, каждый в своей области слыл чудаком. Исчерпав все привычные, простые вопросы, они перешли к явлению куда более сложному. Когда же эти люди обнаружили, что у них есть соратники, то испытали чувство бесконечной благодарности».

Прошло несколько лет. Файгенбаум обитал в скромном жилище, в одной из комнат которого стояла кровать, в другой располагался компьютер, а в третьей помещалась аудиоаппаратура, на которой он слушал свою богатую коллекцию немецких дисков. Во время путешествия в Италию ученый разорился на мраморный кофейный столик, но дорогая вещица не пережила пересылки по почте — Файгенбаум получил лишь обломки мрамора. Вдоль стен были навалены горы книг и бумаг. Откидывая со лба прядь длинных волос — теперь уже каштаново-седых, — Митчелл говорил:

«В двадцатых годах произошло нечто ужасное. Почему-то физики споткнулись на описании окружающего их мира, которое было, в сущности, верным — ведь квантовомеханическая теория до некоторой степени правильна. Мы знаем, как вести расчеты с ее помощью. Она научила нас манипулировать Вселенной. Она поясняет, как сделать компьютер из грязи, как получить химические препараты, пластмассы, все что угодно. Словом, квантовая механика — великолепная вещь, за исключением того, что на определенном уровне она теряет всякий смысл.

Из цепочки образов выпадает звено. Задаваясь вопросом, каково на самом деле значение уравнений, что представляет собой картина мира, построенная данной теорией, получаешь ответ, который не совпадет с нашим ощущением действительности. Мы не можем полагать, будто частица, двигаясь, имеет траекторию. Подобное наглядное представление недопустимо. Чем больше задаешь вопросов о разных непростых вещах — как выглядит мир в зеркале теории? — тем дальше она кажется от наших обычных представлений. Мы запутываемся в противоречиях. Теперь, наверное, мы поймем истинную действительность. Но мы на самом деле еще не знаем, что иного способа обработки информации — способа, который бы не требовал Столь радикального ухода от интуитивного миропонимания, — просто не существует.

Основное установление физики требует для познания Вселенной разъединять ее на фрагменты и рассматривать их отдельно до тех пор, пока не вскроется нечто основополагающее. Затем мы заключаем, что непонятное нам — всего лишь мелочи, детали. Физики полагают, что имеется небольшое число принципов, которые мы можем уяснить, наблюдая объекты в их „чистом“ состоянии. Затем мы собираем детали в более сложную конструкцию, если намереваемся решить более запутанные проблемы. Если можем это сделать.

В конце концов, для постижения всего этого стоит переключить передачу. Нужно переосмыслить свое представление о происходящем. Можно попытаться построить на компьютере модель жидкостной системы. Это уже становится возможным. Но все усилия окажутся напрасными, поскольку происходящее на самом деле не имеет ничего общего с жидкостью или отдельным уравнением. Построенная модель служит лишь общим описанием того, что имеет место в разнообразных системах, работающих как бы сами по себе. Нужно подойти к вопросу с другой стороны.

Взглянув на эту комнату — здесь навален хлам, тут сидит человек, за ним двери, — вы, вооружившись основными законами квантовой механики, используете для описания объектов волновые функции. Однако подобное неосуществимо. Может быть, это под силу Богу, но человек аналитически постигнуть данную проблему не может.

Вопрос о том, что происходит с облаками, уже не относится к чисто академическим. Люди хотят это знать, а следовательно, найдутся деньги на изыскания. Названный вопрос принадлежит по преимуществу к сфере физики. Если мы наблюдаем какое-либо сложное явление, то делаем это так: охватываем как можно больше точек, чтобы определить температуру воздуха, скорость ветра и тому подобные вещи, затем вводим все полученные данные в самую мощную машину, которая нам только доступна, и пытаемся выяснить, что произойдет в дальнейшем. Но все эти действия далеки от реальной жизни».

Файгенбаум, погасив окурок, прикурил следующую сигарету и продолжил:

«Необходимо поискать иные способы. Нужно найти масштабные структуры, соотносимость больших и малых фрагментов. Взгляните на турбулентность в жидкостях и другие сложные системы, в которых хаос проявляется постоянно, подобно некоему закономерному процессу. На определенном уровне еще не важно, каков масштаб этого процесса — охватывает ли он пространство размером с горошину или с баскетбольный мяч. Не имеет значения, где именно он происходит, даже более того — какова его продолжительность. Единственное, что может быть в известной степени универсальным, — масштабные явления.

В некотором смысле искусство представляет собой способ восприятия мира человеком. Очевидно, что никому не известны все детали окружающей нас реальности. Но посмотрите на полотна художников! Они осознали, что далеко не все по-настоящему важно, а затем пригляделись к самым интересным подробностям. Они способны проделать часть моих исследований за меня. Взглянув на ранние работы Ван Гога, можно заметить, что на них изображено огромное количество деталей, в них содержится огромный объем информации. Ему определенно было известно, каково минимальное количество деталей, которое требуется вместить в картину. Обратите внимание на то, как изображали линию горизонта голландские мастера графики начала XVII века. Крошечные коровки и деревца кажутся вполне реальными, и если присмотритесь поближе, заметите, что деревья имеют листья, а в них скрыты еще и небольшие веточки. Между податливыми, мягкими вещами и теми, у которых контуры более определенные, существует некое взаимодействие. Их комбинация так или иначе влечет за собой верное восприятие. Если обратиться к изображению бурных вод Рейсдалом и Тёрнером, то становится понятно, что это можно сделать итерационным способом. Сначала выполняется фон, затем поверху накладывается определенное количество краски, а дальше написанное подвергается изменениям. Для художников турбулентные жидкости всегда обладают свойством масштаба.

Меня на самом деле интересует, как описать облака. Но я не начинал бы с выяснения того, какова плотность здесь, а какова рядом, то есть со сбора всей детальной информации. Думаю, это будет неверно. Человек — и, конечно, художник — воспринимает явления совсем не таким образом. Даже рассмотрение дифференциальных уравнений не решает эту проблему. Удивительное обещание мира состоит в том, что он заключает в себе прекрасные вещи, пленительные, зачаровывающие явления, и благодаря своей профессии мы можем понять их».

Файгенбаум положил сигарету. От пепельницы потянулся дымок, сначала тонким столбиком, а потом — с оглядкой на всеобщность — прихотливыми завитками, устремившимися к потолку.