3. Вероятность события, операции над вероятностями

Вероятностью Р события А при этих условиях будем считать отношение числа случаев m, в пределах которого происходит событие А, к числу N равновозможных событий.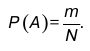

Рассмотрим следующие случаи.

1. m = N, тогда Р(А) = 1. В таком случае событие считают достоверным.

2. т = 0, то есть Р(А) = 0. Не произошло ни одного события, оно является невозможным.

Очевидно, что

0 < Р(А) < 1,

где Р(А) – вероятность появления события А. По мере увеличения количества испытаний (или количества событий)

Р (А) > 1,

то есть вероятность появления событий А возрастает и наоборот.

Над вероятностью можно производить сложение и умножение, как и над числами. Например, для того, чтобы определить вероятность появления одного из трех событии, слагают вероятность каждого из них. Пусть эт?, ими событиями будут события Б, в и С. Тогда вероятность того, что произойдет событие А или В, или С, определяется следующей формулой:

Р(А н Вн С)=Р(А) +Р(В) + Р(С),

где н– логический знак «или», P(A), P(B), P(C) – вероятность каждого из событий А, В или С.

Различают события противоположные: если некоторое событие Д может произойти при непоявлении события А, то события А и Д являются противоположными. Если сложить их вероятности P_А и P_д, то P_А + P_д = 1,

то есть в любом случае произойдет событие А или событие Д.

Событие называется независимым, если его появление не зависит от появления любого другого события. Иначе событие называется зависимым.